Происхождение букв и чисел согласно «Сефер Йецира»
«Лехаим» публикует классическую статью Финеаса Морделла, написанную в 1912 году и посвященную всестороннему исследованию уникального в своем роде еврейского текста — «Сефер Йецира» («Книги Творения»).
Глава 1. Введение
Едва ли существует другая книга в еврейской литературе, за исключением Торы и Талмуда, которая привлекла бы к себе столько комментаторов, как «Сефер Йецира». Это сочинение было предметом глубокого изучения не только мистиков, считавших его источником эзотерических знаний, но также философов и талмудистов . И все же, несмотря на все усилия огромного числа известных исследователей на протяжении более тысячи лет, секреты «Сефер Йецира» остаются нераскрытыми. Многочисленные комментарии к ней скорее сбивают с толку читателя, чем просветляют его. Действительно, создается впечатление, будто каждый толкователь изо всех сил старался вписать в эту небольшую книгу свои взгляды и теории, почти не заботясь о том, согласуются они с текстом или нет.

В nbsp;еврейской литературе нет другой книги такой трудной для понимания, как «Сефер Йецира», ибо изначально она была написана в крайне запутанном, непонятном и полумистическом стиле. Хуже того, комментаторы восьмого или девятого века смешали первоначальную «Сефер Йецира» с ранним комментарием, который можно назвать «Сефер Йецира II». Таким образом, случилось так, что все комментарии, написанные к «Сефер Йецира» с начала десятого века, главным образом основаны на этом смешанном комментарии, а не на оригинальной «Сефер Йецира». Несмотря на все вышеобозначенные трудности с пониманием «Сефер Йецира», решение этих загадок не является невозможным. Причина, по которой они так долго оставались нерешенными, отчасти связана с незнанием еврейской орфографии, на которой основана «Сефер Йецира». Несмотря на многочисленные работы по еврейской орфографии, написанные с начала десятого века, не существует ни одного сочинения, которое могло бы считаться действительно основанным на иврите. Дело в том, что орфография иврита, которой учили и до сих пор преподают, — это орфография арабского, а не иврита. Преподаватели ивритской грамматики под арабским влиянием пришли к убеждению, что правила орфографии, которые арабские мудрецы открыли для языка Корана, применимы и для языка Ветхого Завета. Когда достопочтенный Майер Сульцбергер услышал, что я думаю об ивритской орфографии, он посоветовал мне подробно изучить «Сефер Йецира», которая, по его мнению, представляет собой самую раннюю из сохранившихся грамматик иврита. Обнаружив, что мои взгляды на еврейскую орфографию совпадают со взглядами «Сефер Йецира», я провел ее исчерпывающее исследование. После многих лет глубоких исследований я пришел к выводу, что «Сефер Йецира», как самая ранняя грамматика иврита, содержит не только фундаментальные правила еврейской орфографии, но и сведения о происхождении букв и цифр. Изложение этих находок и является целью нынешнего сочинения .
Первая мишна гласит следующее:
שלשים ושתים נתיבות פליאות חכמה חקק ה׳ צבא‑ות בס͏וֹפֵר וסִ͏פּ͏וּר וסֵפֶר
Тридцать два таинственных пути Г‑сподь, Б‑г Воинств, предписал через Писца, Писание и Свиток .
Тридцать два таинственных пути — это 22 буквы еврейского алфавита, обозначающие 32 звука .
В соответствии с верой древних в Б‑жественное происхождение букв, «Сефер Йецира» объясняет, что 32 пути мудрости были установлены Б‑гом через:
1. (Писца) — человека, которого Б‑г вдохновил изобрести алфавит;
2. (Писание) — буквы;
3. (Свиток) — материал, на котором буквы отображались.
Чтобы показать, как 22 буквы алфавита составляют 32 пути мудрости, автор переходит к разделению букв во второй и последующих мишнайот. Он делит их на простые и двойные звуки, а также на гласные и согласные. Простые буквы он назвал פשוטות и двойные — כפולות; гласные — (אבות=) אמות и согласные — תולדות. Всего они образуют тридцать два звука: двадцать звуков десяти двойных букв и двенадцать — двенадцати простых букв.
«Сефер Йецира» подчеркивает , что количество двойных букв никак не меньше и не больше десяти, а количество простых букв не меньше и не больше двенадцати. «Сефер Йецира» призывает нас исследовать и изучать буквы, чтобы мы могли получить ясное представление о предмете. Это доказывает, что в то время, когда была написана книга, природа всех букв или некоторых из них была неправильно понята. Мы знаем, действительно, что в то время, когда был сделан греческий перевод Библии, считалось, что буква ע, например, может быть транслитерирована как э, а или г, и переводчики, соответственно, переводили ее по‑разному, используя один из этих трех звуков.
Неоднократно выдвигались аргументы в пользу того, что еврейское ע имело не только звук арабского ء, но также и ġ. Однако, согласно «Сефер Йецира», ע — это простая буква. Она не может обозначать больше одного звука. Более того, если ע изначально была только гласной и не обозначала звука ġ, как утверждает Иероним [Стридонский] , она могла бы иметь только один гласный звук. Если мы припишем ей звук а, невозможно, чтобы она также имела звук э, или о, или какой‑либо еще. Кроме того, согласно «Сефер Йецира», буквы צ, ט, ח также являются простыми буквами и каждая из них должна иметь лишь один звук, а не два, как в арабском языке.
Автор «Сефер Йецира», по‑видимому, предостерегал читателей как раз от тех самых ошибок и искажений, которые допускали все авторы сочинений по грамматике иврита. Разделив 22 еврейские буквы на 10 двойных и 12 простых, обозначающих 32 звука, автор хотел прояснить, насколько еврейский алфавит отличается от алфавита, который известен как арабский и который сами арабы называли «сури». Под сури, очевидно, имелся в виду ассирийский язык. Так называемый арабский алфавит первоначально состоял всего из 17 букв. По‑видимому, первоначально он был изобретен для обозначения ассиро‑вавилонского языка, состоявшего из 17 или 18 звуков. Отсюда и название сури. Когда арабы, чьим первоначальным алфавитом был химьярит, состоящий из 28 букв, переняли алфавит сури, они придали некоторым буквам сури два или даже три звука, и каждая такая буква теперь считается за две или три буквы.
Так как, согласно «Сефер Йецира», еврейский алфавит состоит из 10 двойных букв и 12 простых, то каждой двойной букве должно быть приписано два звука, а каждой простой букве — только один звук, независимо от их значения в арабском языке.
Наиболее точная транслитерация двойных букв выглядит следующим образом: א = э, א = о, ב = б, ב = в, ג = г, ג = дж, ד = д, ד = th, ו = у, ו = в, כ = к, כ = х, פ = п, פ = ф, ר = р, ר = р или арабская ġ, ש = ш, ש = ж, ת = т, ת = th.
Наиболее точная транслитерация простых букв выглядит следующим образом: ה = h, ז = з, ח = х, ט = т, י = й, ל = л, מ = м, נ = н, ס = с, ע = а, צ = ц, ק = к.
Дав такое разделение букв, «Сефер Йецира» показывает, как из этих 22 букв могут быть образованы все слова, которые когда‑либо существовали или когда‑либо будут построены . Целью автора было подчеркнуть превосходство алфавитного письма над безалфавитным письмом (идеографическим или слоговым), употребляемым всеми народами древности, да и теперь значительной частью человечества. Если мы расположим в алфавитном порядке все двухбуквенные комбинации, как предписывает «Сефер Йецира», соединив сначала букву א со всеми буквами, затем ב со всеми буквами и т. д., в результате должен получиться список из 484 комбинаций (222 = 484).
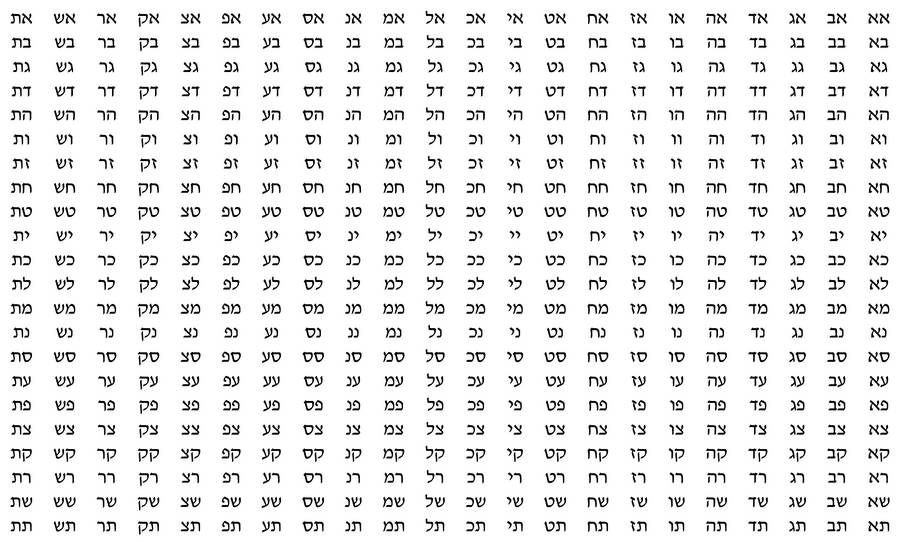
Более того, выражением
וחוזר הגלגל פנים ואחור וסימן לדבר עין למעלה ענג ועין למטה נגע
[…и круг вращается вперед и назад; таким образом, в ענג [наслаждении] ע в начале; в נגע [язва] же ע в конце]
в мишне 7 «Сефер Йецира» указывает на то, что двухбуквенные комбинации могут быть положены в основу всех трехбуквенных комбинаций. Если мы захотим расположить все трехбуквенные комбинации, которые можно составить из 22 букв ивритского алфавита, их число будет 223, или 10 648. Для наглядного перечисления всех таких комбинаций понадобилось бы составить 22 таблицы двухбуквенных сочетаний, оставляя между каждыми двумя сочетаниями достаточно места для добавления буквы. В первой таблице нужно было бы добавить א в начале каждой двухбуквенной комбинации, и в результате получилась бы полная таблица из 484 трехбуквенных комбинаций, начинающихся с א; в другом случае таким же образом добавлялась бы буква ב, образуя полную таблицу из 484 трехбуквенных комбинаций с буквой ב в начале. Поступив таким образом и с остальными буквами, мы бы построили все возможные трехбуквенные комбинации, которые можно составить из 22 букв. С таким подходом мы экономим две трети трудозатрат, необходимых в противном случае, поскольку прибавление третьей буквы составляет лишь одну треть труда, необходимого для получения всех трехбуквенных комбинаций. Если мы захотим записать все четырехбуквенные комбинации, которые можно составить из 22 букв, нам нужно будет только сделать 22 копии всех трехбуквенных комбинаций, оставив достаточно места между двумя последовательными комбинациями для добавления новой буквы. Далее, прибавляя букву א в начале каждой трехбуквенной комбинации, мы получим 10 648 четырехбуквенных слов, начинающихся на א. То же самое упражнение мы проведем с буквой ב и так далее со всеми остальными 20 буквами алфавита. Эта процедура обеспечит нас 224 = 234 256 словами. Количество пятибуквенных слов будет равно 5 153 632.
Значения первых 12 степеней числа 22 дают следующие количества полученных комбинаций:
222 = 484
223 = 10 648
224 = 234 256
225 = 5 153 632
226 = 113 379 904
227 = 2 494 357 888
228 = 54 875 873 536
229 = 1 207 269 217 792
2210 = 26 559 922 791 424
2211 = 584 318 301 411 328
2212 = 12 855 002 631 049 216
Таким образом, очевидно, что 22 буквы допускают бесконечное количество комбинаций и расположений, достаточных для обозначения не только всех мысленных понятий, но и всех слов на всех языках.
Согласно «Сефер Йецира», те же результаты можно получить, добавив букву в конце каждой комбинации. Когда буква добавляется в начале, процесс называется поворотом таблицы перед [буквой] (וחוזר הגלגל פנים), таблица поворачивается перед каждой буквой, как נג поворачивается перед ע и становится ענג. Когда же буква добавляется в конце, операция называется поворотом таблицы за [буквой] (וחוזר הגלגל אחור), таблица поворачивается за буквой, как נג поворачивается за ע и дает слово נגע. Так же как оба слова ענג и נגע могут быть получены из נג и ע, любая трехбуквенная комбинация может быть получена из соответствующей двухбуквенной добавлением недостающей буквы в начале либо в конце. Четырехбуквенные слова аналогичным способом строятся из трехбуквенных, и во всех этих случаях уже необязательно строить полные таблицы, если однажды мы уже поняли сам принцип построения.
Как из 22 букв образуется бесконечное количество слов (без повторов букв. — Примеч. перев.), «Сефер Йецира» показывает посредством перестановок, при которых буквы никогда не повторяются, а лишь меняют свои места. Из двух букв два двухбуквенных слова образуются как אב и בא. Из трех букв образуются шесть трехбуквенных слов: אבג, אגב, באג, בגא, גאב, גבא. Из четырех букв образуется 24 четырехбуквенных слова: בגדא, בגאד, באדג, באגד, אדגב, אדבג, אגדב, אגבד, אבדג, אבגד, דאגב, דאבג, גדבא, גדאב, גבדא, גבאד, גאדב, גאבד, בדגא, בדאג, דגבא, דגאב, דבגא, דבאג. Из пяти букв могут быть составлены 120 уникальных пятибуквенных слов, из шести букв — 720 шестибуквенных слов, из семи букв — 5040 семибуквенных слов . «Сефер Йецира» приводит факториалы до семи и завершает мишну словами: «Иди и считай дальше то, что неспособны произнести уста и неспособно услышать ухо».
Факториалы первых 12 чисел дают следующие значения:
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720.
7! = 5040
8! = 40 320
9! = 362 880
10! = 3 628 800
11! = 39 916 800
12! = 479 001 600.
Значения факториалов до 36 приведены в Энциклопедии Риса в статье «Шифр». Рассмотрение мишной перестановок было хорошо объяснено всеми комментаторами, особенно (С.) [Ш.] Донноло.

У. nbsp;Стэнли Джевонс по поводу перестановок отмечает :
Таким образом, буквы будут образовывать разные перестановки в зависимости от того, стоит ли А первой, второй или третьей; определив место А, мы можем выбрать одно из двух мест для Б; и тогда остается лишь одно место для В. Соответственно, количество легитимных перестановок этих букв будет всего 3 × 2 × 1, или 6. С четырьмя предметами или буквами А, Б, В и Г у нас будет четыре возможности выбора места для первой буквы, три для второй, два для третьей и одно для четвертой, так что всего будет 4 × 3 × 2 × 1, или 24 перестановки. Одно и то же простое правило применимо ко всем случаям; начиная с целого общего числа мест, на каждом шаге умножаем [уже полученный промежуточный результат] на это число, уменьшенное на единицу.
Далее он добавляет:
Многие писатели время от времени отмечали необычайную величину чисел, с которыми мы имеем дело в таком подсчете. Таке подсчитал, что 24 буквы алфавита могут быть расположены более чем в 620 (тысячах триллионов) [квадриллионах] порядков; а Шотт заметил, что, если бы написанием этих перестановок были бы одновременно заняты (тысяча миллионов) [миллиард] людей и каждый человек заполнял бы каждый день сорок страниц с сорока перестановками в каждой, они бы не справились с этой задачей, поскольку они написали бы только 584 (тысячи триллионов) [квадриллионов] вместо 620 (тысяч триллионов) [квадриллионов].
Продолжение следует
Комментариев нет:
Отправить комментарий